Advances in diagnostic instruments, lens materials and manufacturing technology have paved the way for innovative products that complement our contact lens armamentarium. Over the last two decades, we have enjoyed the commercialization of low-cost cast-molded lenses, improved optics and improved in vivo wetting, as well as oxygen-permeable soft, rigid and hybrid lenses.
But, there still remains a significant segment of patients with ametropia and ocular surface disease who struggle with limited wearing time or incomplete correction of their refractive error and presbyopia. Hybrid lenses are a successful option for many of these patients; even so, occasional flexure, the need for greater oxygen transmission in the soft skirt portion of the lens and the lack of a non-rotating design have limited hybrid lens use.
A rigid lens that makes contact only with the sclera and clears the entire cornea and limbus has a number of advantages and benefits over corneal contact lenses, hydrogel lenses and hybrid lenses. The primary advantage of rigid lenses for regular and irregular corneal surfaces is a stable and more complete optical correction of lower- and higher-order aberrations. Mini-scleral lenses can be rotationally stabilized to facilitate front surface toric correction, decentered multifocal designs, and higher order aberration correction. The circumferential interface with the bulbar conjunctiva deters the foreign body migration that is otherwise a disadvantage of corneal contact lenses.
Rigid lenses that make contact with the bulbar conjunctiva and cover the sclera have a long history in ophthalmic treatment and refractive error correction. They are known by many names: scleral shells, scleral contact lenses, or haptic lenses, and more recently, semi-scleral, mini-scleral, and corneo-scleral lenses. Efforts have been made to classify modern scleral lenses based on their overall diameter and their zones of contact with regard to corneal contact, scleral contact or both.4
Practitioners continue to express a need for rigid lens optics with all day comfort. As a result, there is a renewed interest in large diameter GP lenses. Most of the reported use appears to be limited to the correction of irregular astigmatism of corneal origin and for patients with ocular surface disease. Unfortunately, it is frequently reported that the fitting of scleral contact lenses is challenging, time consuming and often involves multiple diagnostic sets and several re-orders of lenses for a respective eye.5,6
Recently, the confluence of improved metrology for measuring ocular contour, computer numerically controlled lathes, and lens materials with improved mechanical properties and ultra-high oxygen permeability has stimulated renewed interest in mini-scleral contact lenses.
Limiting Factors
What factors limit the increase in use of scleral lenses?
For one, lens diameter brings with it challenges. Lenses greater than 18mm in diameter provide a wider zone of scleral contact and present challenges with regard to stagnation and difficulty in lens removal. Recent research in measuring scleral geometry explains the need to design lenses that are larger than 18mm. However, at the same time, practitioners express the desire to fit lenses that are smaller.
Another challenge that hinders adoption is the tendency for lens manufacturers to withhold specific parameter information for the lenses. Further, the lexicon used for referencing the zones and geometry of the lenses, along with the general negative history of scleral lenses, sends many practitioners running.
Add to this the difficult and time-consuming fitting, the reduced comfort of the lenses (vs. soft lenses), persistent peripheral bubbles and tear stagnation, and scleral lenses may not sound appealing to you or your patients at all. Not to mention, best-corrected acuity can be subverted by lens flexure and complications with the rotational stability needed to correct the full continuum of lower-order refractive errors.
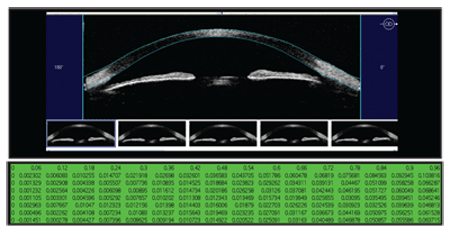
|
| 1. Measurement is the first step to modulation. To better understand scleral contour, Jim Schweigerling, Ph.D., used experimental software to measure sagittal height every 60 µm from the center of the eye out to 15.5mm.
|
Challenge: Solve the Problems
The first step in the effort to improve large-diameter lens design and the creation of a low-chair time fitting system is measurement. Clinicians involved with scleral lens fitting struggle with the absence of instrumentation for measuring scleral contour. In the recent past, Scheimpflug photography (Oculus, Pentacam) and anterior segment optical coherence tomography (Visante OCT, Carl Zeiss Meditec) have been suggested.7,8 These instruments provide an image of the cornea and sclera out to a chord diameter of 14mm to 16mm that could be useful for individual patient baseline measurements. Neither technology currently incorporates software that precisely measures the elevation or shape of the eye to the limits of the image. The Visante does offer the ability to manually draw lines on the OCT image and provides the length of these lines; however, measuring corneal sagittal height by this means is tedious at best.
So, one alternative is to manually measure sagittal heights and local slopes with these instruments to assist in the design of lenses. But, the cost of the instruments and the time consumption of manual measurement will likely limit the application of these technologies in the expansion of scleral lens fitting.
Distribution studies that use custom software are a means of understanding scleral contour in the absence of individual, clinician-owned instruments. Such a study was conducted at the University of Arizona by Jim Schwiegerling, Ph.D., in an effort to understand the geometry of the mean eye in a normal population along with an analysis of the standard deviation (figure 1).
A New Lens Design
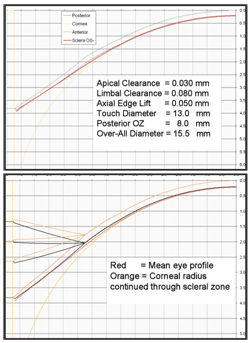
2. Design criteria for the 15.5mm overall diameter lens. Top, the ideal geometry with prescribed apical clearance, limbal clearance and axial edge lift. Bottom, a single convex radius can be prescribed with selected "curve angles" to produce the desired edge lift.
William Meyers, Ph.D. and I used these data, postulated design concepts and discovered some shortcomings in current designs. In our design, we aimed to achieve complete clearance of the cornea and limbus. Our model provides for 30µm of clearance over the central cornea and up to 80µm of clearance at a chord diameter of 10.5mm. The model calls for a maximum scleral touch at a chord diameter of 13.5mm and an axial lift of 50µm at the edge of a lens. The lens has an 8.0mm optic zone joined to a second zone that is 1.25mm wide. This second zone joins at 10.5mm to a 2.5mm-wide peripheral zone for a resultant overall diameter of 15.5mm (figure 2).
We quickly discovered that it’s not possible to achieve these design features with the use of a peripheral zone that is either conventionally concave to the eye or un-curved (tangential). If the goal is to avoid contact with the cornea (or accept feather touch in the central cornea) and have clearance at the beginning of the peripheral zone and over the limbus with freedom from scleral impingement, the discovered scleral contour of the full distribution of eyes demonstrates the requirement for a peripheral zone that is convex to the eye (figure 3).
So, we selected a fixed convex curve radius for the landing zone of the 15.5mm diameter lens. The curve is controlled by a landing zone angle (LZA) to provide the variation needed to fit the full continuum of eyes. The angle designated as the LZA is the angle between the extension of the chord through the junction medial to the zone and a chord connecting the arc of the curve of the landing zone. We determined that a mean LZA for the 15.5mm-diameter lens is 54º with a range from 48º to 60º.
The fitting objectives are achieved when the angle selected demonstrates clearance over the peripheral cornea at the medial junction of the landing zone and clearance at the edge of the lens over the sclera.
The proper LZA can be selected without any instrumentation by the use of a small set of diagnostic lenses that exceed the depth of any eye and make contact only with the sclera. A lens with too great an angle will demonstrate no edge lift while a lens with too shallow an angle will have excessive edge lift and will touch the cornea at the medial aspect of the landing zone (10.5mm chord).
Selecting the Lens Parameters
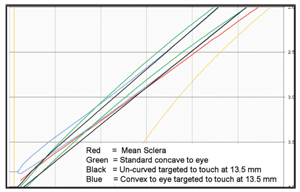
3. Simultaneous clearance at the 10.5mm chord and at the edge requires a convex-to-the-eye peripheral zone.
We constructed a minimum three-zone lens that includes the peripheral-scleral landing zone, a medial connecting zone (a “return zone”) and a central optic zone. The optic zone has a fixed-width, conventional base curve that may be determined with the aid of keratometry or corneal topography. The return zone also has a fixed width, and its depth is determined from the elevation data from corneal topography and the selected central base curve.
The recommended base curve for regular corneas is 0.1mm (0.50D) flatter than the flattest keratometry value. For irregular corneas, the suggested base curve is the reference sphere calculated by the corneal topography software. The reference sphere is a curve that, if suspended in the cornea, would allow the highest point of the cornea over an 8mm chord diameter to be approximately the same amount above the sphere as the lowest point of the cornea would be below it. Such a sphere, when elevated above the cornea, will have the least clearance over the lowest and highest points.
The return zone depth (RZD) is calculated using corneal elevation data. To determine the RZD, the height of the lens above the cornea at 8mm and the elevation of the cornea at 10.5mm must be known. The corneal topography elevation data is used to determine the clearance of the lens at the chord of the optic zone diameter (8.0mm). The original design paradigm calls for a clearance above the highest point on the cornea of at least 30µm; so, the starting base curve is elevated above the cornea by this amount. Since we know the corneal elevation at the 8mm chord, the selected base curve and the need to raise the base curve above the cornea by 30µm, we can now calculate the elevation of the lens above the cornea at the 8mm chord. This is the junction where the RZD originates.
The elevation of the cornea at the next junction, at the 10.5mm chord, must be discovered to complete the calculation for the RZD. Most placido-based topographers are limited to gathering data out to approximately 9mm. But, the outer diameter of the return zone is 10.5mm. So, a topography software algorithm can use the elevation at the 9mm chord and the local slope from 8mm to 9mm to extrapolate the approximate elevation at 10.5mm. The RZD is the total change of sagittal depth of the lens from the chord of 8mm to the chord of 10.5mm.
Recall that the LZA is found by applying diagnostic lenses until the optimum angle demonstrates clearance at the 10.5mm junction and edge clearance. Visible clearance is of the order of 30µm to 80µm. Using this assumption and the extrapolated corneal topography data, software can locate the position of the lens above the 10.5mm chord and calculate the required RZD to connect this point with the location of the lens at the 8mm point when the optic zone is properly elevated above the cornea.
The final result defines the parameters of three zones of a lens: the base curve of an 8mm optic zone, the return zone depth of an annulus that’s 1.25mm wide, and the landing zone angle of an annulus that’s 2.5mm wide.
Orientational Stability and Flexure Management
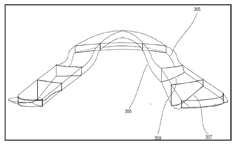
4. The dual-axis feature in the return zone or landing zone allows the base curve to remain spherical while the lens periphery varies independently to accommodate scleral contour, controlling flexure and providing orientational stability.
We made an additional discovery with the scleral contour data when we took measurements in multiple meridians: The comparison of intra-eye data for vertical, horizontal and two oblique measurements revealed that the sclera is not isometric in elevation circumferentially. Rather, like the cornea, the sclera trends toward being deeper vertically than horizontally. There is some variance in the axis of the shallowest portion of the sclera and in some cases the shallowest and deepest meridians are not orthogonal.
There is an opportunity, if not a requirement, to design the lenses with a dual axis RZD and/or LZA. While keeping the base curve spherical, one semi-meridian is designed to have a deeper RZD and/or LZA than the others. Failure to implement this dual-axis feature will result in lens flexure similar to that observed in GP and hybrid lenses over the years. The dual axis feature allows the periphery of the lens to match the high and low areas of the sclera. This match fills in the elevation difference and prevents the lens from flexing. The amount of difference between the deep and shallow RZD semi-meridians can be varied for precise flexure control while keeping the base curve radius spherical and without adding extra thickness to the lens (figure 4).
The dual-axis feature fortuitously also serves to provide orientational stability without the addition of prism ballast, double-slab off or other thin/thick zone design features. The addition of a lens mark to indicate the deep meridian of the lens provides the basis for over-refraction and prescribing a front surface cylinder. Success in orientational stability and lens registration also paves the way for higher-order aberration correction, as well as pupil or visual-axis registration of presbyopic lens designs.
Time to Troubleshoot
Mid-peripheral bubbles occur when the lens is more than roughly 100µm from the cornea. Unless the lens completely seals on the sclera, a design in which the base curve and second zone depart from the cornea by more than 100µm will result in bubbles. Bubbles occur frequently when you try to place a rotationally symmetrical lens on an irregular, rotationally asymmetric cornea with significant elevation differences. Even so, the use of the reference sphere as a base curve will minimize the difference. Another feature that can be incorporated is the use of different geometries in the connecting return zone.
It is possible to use two or more different geometries to create the same sagittal depth. In this manner, volume can be modulated while keeping sagittal depth constant. The RZD can be achieved with a concave curve, convex curve, straight line or, in the usual case with this design, a third-order polynomial. One meridian that has greater clearance can be “filled in” while maintaining the same sagittal depth through the use of a different geometry.
Tear stagnation reported with full scleral lenses can be modulated with tear channels. Stagnation with mini-scleral lenses (less than 16mm in overall diameter) may be due to the scleral impingement or junction seal-off that occurs with lenses that demonstrate clearance at 10.5mm and feature concave-to-the-eye or tangential peripheral zones. The objective of the convex-to-the-eye peripheral zone is a demonstrated edge clearance with a concomitant clearance at the 10.5mm chord. Clinical observations support that lenses of this design are free to move on push-up and are free of scleral impingement when the proper LZA is selected. The free movement on push-up associated with edge clearance also allows for easier lens removal. Patients report the ability to remove the lenses by use of the lids as levers in a manner similar to a” scissors technique” for corneal GP lenses.
The Final Product
This patent-pending, novel large-diameter lens will be available through multiple laboratories and is manufactured in Paragon HDS 100 material with an ISO Dk of 100. Fitting this new lens requires a standard corneal topographer and the use of software provided by Paragon Vision Sciences through their authorized independent laboratories.
The legacy of scleral lenses discourages many practitioners from fitting them. But, these design features and this fitting system, based on discovered scleral contour data, open the door to helping patients who heretofore have not been satisfied with the comfort and vision of conventional offerings.
Dr. Legerton is an author, lecturer, inventor and consultant to the ophthalmic industry. He was the managing partner of a seven-doctor multispecialty practice in San Diego, where he provided clinical care for 26 years. He is the co-founder of SynergEyes, and his 22 issued U.S. patents and more than 30 pending applications include inventions for corneal refractive surgery for presbyopia, Paragon CRT, hybrid contact lenses, regulation of myopia progression, scleral contact lenses and contact lenses for wearable displays.
1. Pearson, RM. The Samisch Case and the Mullers of Wiesbaden. Optom Vis Sci. 2009;86(2)157-64.
2. Schaeffer, J, Beiting, J. The Early History of Contact Lenses. Rev Optom. 2007 Sep 15;144(9):76-82.
3. Boston Foundation for Sight. Available at:
www.bostonsight.org/doctors.htm (Accessed December 18, 2009).
4. Sindt, C. Basic Scleral Lens Fitting and Design. Cont Lens Spect. 2008; 23(10):32-36.
5. Ye P, Sun A, Weissman BA. Role of mini-scleral gas-permeable lenses in the treatment of corneal disorders. Eye Cont Lens. 2007;33(2):111-3.
6. Thakrar V. Scleral contact lenses: then and now. Eye Care Review. 2007;(2):47-8.
7. Gemoules G. A novel method of fitting scleral lenses using high resolution optical coherence tomography. Eye Cont Lens. 2008;34(2):80-83.
8. Van der Worp E. New technology in contact lens practice. Cont Lens Spect. 2010;(2):22-9.

